函數圖形橫跨了代數與幾何,能將變數之關係式化為具體的圖像,反之,也能將幾何以簡潔的代數式來描述。函數圖形的應用相當廣泛,任何學科若需要分析變數之間的相互關係,就可派上用場,也可以解決生活中遇到的問題,例如:手機通話費與通話時間的關係、彈簧與掛重之間的關係等。
在國中階段,函數圖形的教學,會先讓學生理解二元一次方程式的圖形畫法,再循序教授一次函數和二次函數的圖形。在傳統教學,老師會在黑板上,以一個簡單的函數式為例,一邊講解,一邊畫出其相對應的函數圖形,此種方式,對於剛接觸函數的學生而言,往往僅能理解局部概念;對老師而言,也會因為時間的因素、板書的限制,無法將函數式與函數圖形之間的關係,作出完整的解說。
為了讓學生完全理解函數圖形,葛倫老師特別製作國中課程的函數圖形動態數學,透過程式的互動功能,學生可以經由改變參數值,直接觀察到圖形的變化,從而建立完整的函數圖形觀念。這一系列的動態數學,除了方便學生自學,也非常適合老師在課堂上引用來解說,不但可以節省課堂上繪圖的時間,也可以將函數圖形的性質作精準且動態的說明。
歡迎分享給需要的老師和學生來使用↓
Live數學學習網─函數圖形動態數學
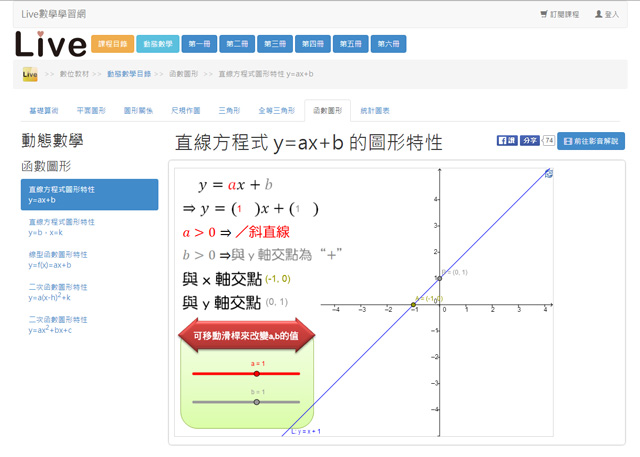
直線方程式圖形特性 y=ax+b https://goo.gl/279KFo
直線方程式圖形特性 y=b,x=k https://goo.gl/D445P4
線型函數圖形特性 y=f(x)=ax+b https://goo.gl/w7ATrF
二次函數圖形特性 y=a(x-h)2+k https://goo.gl/Ftxoed
二次函數圖形特性 y=ax2+bx+c https://goo.gl/W7Cakx

