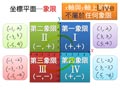
坐標平面上的象限
【圖一】象限
$x$ 軸與 $y$ 軸將直角坐標平面分成四個區域,我們把四個區域都稱為象限。如【圖一】,依逆時針方向分為:
- 第一象限 : $x$ 坐標為正, $y$ 坐標為正。
- 第二象限 : $x$ 坐標為負, $y$ 坐標為正。
- 第三象限 : $x$ 坐標為負, $y$ 坐標為負。
- 第四象限 : $x$ 坐標為正, $y$ 坐標為負。
★ $x$ 軸與 $y$ 軸上的點不屬於任何象限。
例
【圖二】例子─點在坐標軸或象限
| 點 | 行進方向 | 位置 | 記號 | 坐標軸 或象限 |
$x$ 坐標 (橫坐標) |
$y$ 坐標 (縱坐標) |
|---|---|---|---|---|---|---|
| $A$ | 從原點 $O$ 出發,沿 $x$ 軸的正向走 $3$ 個單位,到達 $A$ 點 | $(3,0)$ | $A(3,0)$ | $x$ 軸 | $3$ | $0$ |
| $B$ | 從原點 $O$ 出發,沿 $y$ 軸的正向走 $4$ 個單位,到達 $B$ 點 | $(0,4)$ | $B(0,4)$ | $y$ 軸 | $0$ | $4$ |
| $R$ | 從原點 $O$ 出發,沿 $x$ 軸的正向走 $3$ 個單位,再朝 $y$ 軸的正向走 $4$ 個單位,到達 $R$ 點 | $(3,4)$ | $R(3,4)$ | 第一象限 | $3$ | $4$ |
| $C$ | 從原點 $O$ 出發,沿 $x$ 軸的負向走 $3$ 個單位,到達 $C$ 點 | $(-3,0)$ | $C(-3,0)$ | $x$ 軸 | $-3$ | $0$ |
| $D$ | 從原點 $O$ 出發,沿 $y$ 軸的負向走 $4$ 個單位,到達 $D$ 點 | $(0,-4)$ | $D(0,-4)$ | $y$ 軸 | $0$ | $-4$ |
| $S$ | 從原點 $O$ 出發,沿 $y$ 軸的負向走 $3$ 個單位,再朝 $y$ 軸的負向走 $4$ 個單位,到達 $S$ 點 | $(-3,-4)$ | $S(-3,-4)$ | 第三象限 | $-3$ | $-4$ |
觀念影片
|
3
|
(3)坐標平面上的象限4:30 |
|

