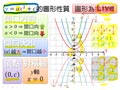
y=ax2＋c的圖形性質

$$y=2x^2+2$$

二次函數 y=2x^2+2 的圖形

 

$$y=-2x^2-2$$

二次函數 y=-2x^2-2 的圖形

 

 

$$y=x^2+1$$

二次函數 y=x^2+1 的圖形

 

$$y=-x^2-1$$

二次函數 y=-x^2-1 的圖形

 

 

$$y=\dfrac12x^2+\dfrac12$$

二次函數 y=0.5x^2+0.5 的圖形

 

$$y=-\dfrac12x^2-\dfrac12$$

二次函數 y=-0.5x^2-0.5 的圖形

 

 

函數式為 $y=f(x)=ax^2+c\;(a\neq 0)$ 的二次函數圖形為拋物線，有以下性質：

  1. 開口方向：若 $a\gt 0$ ，則圖形開口向上；若 $a\lt 0$ ，則圖形開口向下。
  2. 開口大小：若 $|a|$ 越大，則圖形的開口越小；若 $|a|$ 越小，則圖形的開口越大。
  3. 頂點： $(0,c)$ 。
  4. 對稱軸： $y$ 軸（即 $x=0$ ）。

觀念影片