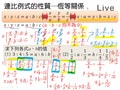
連比例式的性質─恆等關係

若 $a$ 、 $b$ 、 $c$ 都不為 $0$ ，且 $x:y:z=a:b:c$ ，則：

1. $\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}$
2. $x:a=y:b=z:c$

說明

$\because x:y:z=a:b:c$

$\therefore x:y=a:b$ $\Rightarrow \dfrac{x}{a}=\dfrac{y}{b}$ ，且 $y:z=b:c$ $\Rightarrow \dfrac{y}{b}=\dfrac{z}{c}$

$\therefore \dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}$ ，即 $x:a=y:b=z:c$

例 求下列各式 $a$ 、 $b$ 的值

1. $3:4:5=a:6:b$
2. $\dfrac12:a:\dfrac13=b:\dfrac14:\dfrac15$

解

1. $\because 3:4:5=a:6:b$

$\therefore \dfrac{3}{a}=\dfrac{4}{6}=\dfrac{5}{b}$

由 $\dfrac{3}{a}=\dfrac{4}{6} \Rightarrow a=\dfrac92$

由 $\dfrac{4}{6}=\dfrac{5}{b} \Rightarrow b=\dfrac{15}{2}$

2. $\because \dfrac12:a:\dfrac13=b:\dfrac14:\dfrac15$

$\therefore \dfrac12:b=a:\dfrac14=\dfrac13:\dfrac15$

由 $\dfrac12:b=\dfrac13:\dfrac15 \Rightarrow b=\dfrac{3}{10}$

由 $a:\dfrac14=\dfrac13:\dfrac15 \Rightarrow a=\dfrac{5}{12}$