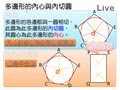
多邊形的內心與內切圓
定義:若一多邊形的每邊都能與多邊形內部的一個圓相切,則此圓稱為多邊形的內切圓,圓心稱為此多邊形的內心,而此多邊形稱為圓外切多邊形。
例 如圖一, $O_1$ 、 $O_2$ 、 $O_3$ 分別為各多邊形的內心。
$$圖一$$
★ 並非所有的多邊形都有內切圓。
性質:
(1) 圓外切多邊形每一角的角平分線會交於一點,此交點即為多邊形的內心,且內心到此多邊形的各邊等距離,此距離為內切圓的半徑,如圖二所示。
$$圖二$$
(2) 若一四邊形兩對對邊之和相等,則此四邊形為圓外切四邊形,其內切圓的圓心為四邊形的內心。
例 如圖三, $\overline{AB}+\overline{CD}=\overline{BC}+\overline{DA}$ ,則四邊形 $ABCD$ 為圓外切四邊形, $O$ 點為四邊形 $ABCD$ 的內心。
$$圖三$$
判別:
若一多邊形各角的角平分線同時交於一點,則此多邊形為圓外切四邊形。
觀念影片
|
2
|
(2)多邊形的內心與內切圓6:40 |
|

