三角形的外心
定義:三角形三邊的中垂線會交於一點,此點稱為三角形的外心。
例 如圖一,若三直線 $L$ 、 $M$ 、 $N$ 分別為 $\overline{AB}$ 、 $\overline{BC}$ 、 $\overline{CA}$ 的中垂線,則交點 $O$ 即為 $\triangle ABC$ 的外心。
$$圖一$$
性質:外心到三角形的三頂點等距離,所以外心也是此三角形外接圓的圓心。
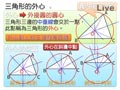
外心的位置:
$$銳角三角形\\在三角形內部$$
$$直角三角形\\在斜邊的中點$$
$$鈍角三角形\\在三角形外部$$
觀念影片
|
1
|
(1)三角形的外心7:57 |
|

