三角形的內心與頂角角度關係

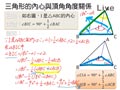
【已知】如圖一， $I$ 為 $\triangle ABC$ 的內心

【求證】 $\angle BIC=90^{\circ}+\dfrac12\angle BAC$

【證明】

$\because I$ 是 $\triangle ABC$ 的內心

$\therefore \angle 1=\dfrac12\angle ABC$ ， $\angle 2=\dfrac12\angle ACB$

在 $\triangle BIC$ 中

$\begin{array} {rl} \angle BIC & =180^{\circ}-\angle 1-\angle 2 \\ &=180^{\circ}-\dfrac12\angle ABC-\dfrac12\angle ACB \\ &=180^{\circ}-\dfrac12(\angle ABC+\angle ACB) \\ &=180^{\circ}-\dfrac12(180^{\circ}-\angle BAC) \\ &=90^{\circ}+\dfrac12\angle BAC \end{array}$

故得證