圓心角與弧的度數
圓心角:在平面上一圓,以圓心為頂點,兩半徑為邊所夾的角稱為圓心角。
例 如圖一,若 $\overline{OA}$ 、 $\overline{OB}$ 為圓 $O$ 的兩半徑,則 $\angle AOB$ 就稱為圓心角。其中, $\stackrel{\Large \frown}{AB}$ 稱為圓心角 $\angle AOB$ 所對的弧。
$$圖一$$
弧:如圖二,圓 $O$ 上任意兩點 $A$ 、 $B$ ,把圓分成兩個弧,其中小於半圓的弧稱為劣弧,以 $\stackrel{\huge \frown}{ACB}$ 表示,通常記為 $\stackrel{\Large \frown}{AB}$ ;大於半圓的弧稱為優弧,以 $\stackrel{\huge \frown}{ADB}$ 表示。
★ $\stackrel{\Large \frown}{AB}$ 代表弧的度數或弧的長度。
$$圖二$$
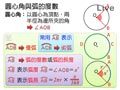
例 如圖三,若圓 $O$ 的半徑為 $r$ , $\stackrel{\Large \frown}{AB}$ 的度數即為 $\angle AOB$ 的度數,所以 $\stackrel{\Large \frown}{AB}=\angle AOB=x^{\circ}$ , $\stackrel{\Large \frown}{AB}$ 的長度即為圓周長 $\times \dfrac{x}{360}$ , 所以 $\stackrel{\Large \frown}{AB}$ 的長度 $=2\pi r\times \dfrac{x}{360}$
$$圖三$$
觀念影片
|
1
|
(1)圓心角與弧的度數5:47 |
|

