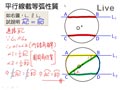
平行線截等弧性質
例 如圖,已知 $L_1\; /\!/ \;L_2$ ,試說明 $\stackrel{\Large \frown}{AC}=\stackrel{\Large \frown}{BD}$ 。
說明
連接 $\overline{BC}$ ,
$\because L_1\; /\!/ \;L_2$
$\therefore \angle ABC=\angle BCD$ (內錯角相等)
又 $\because \angle ABC=\dfrac12 \stackrel{\Large \frown}{AC}\;$ , $\angle BCD=\dfrac12 \stackrel{\Large \frown}{BD}$ (圓周角性質)
$\Rightarrow \; \dfrac12\stackrel{\Large \frown}{AC}=\dfrac12\stackrel{\Large \frown}{BD}$
$\Rightarrow \; \stackrel{\Large \frown}{AC}=\stackrel{\Large \frown}{BD}$
觀念影片
|
5
|
(5)平行線截等弧性質5:37 |
|

