圓內角之意義與性質
意義:若兩弦交於圓內一點,則此兩弦所形成的交角稱為圓內角。
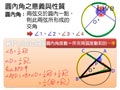
例 如圖一, $\angle 1$ 、 $\angle 2$ 、 $\angle 3$ 、 $\angle 4$ 稱為圓內角。
$$圖一$$
性質:圓內角度數等於其所夾兩弧度數和的一半。
例 如圖二, $\angle APD$ 為圓內角,
試說明 $\angle APD=\dfrac12(\stackrel{\Large \frown}{AD}+\stackrel{\Large \frown}{BC})$ 。
$$圖二$$
說明
如圖三,連接 $\overline{BD}$ 。
$\Rightarrow \; \angle ABD=\dfrac12\stackrel{\Large \frown}{AD}$ , $\angle CDB=\dfrac12\stackrel{\Large \frown}{BC}$ (圓周角性質)
在 $\triangle BPD$ 中
$\begin{array} {rl} \angle APD & =\angle ABD+\angle CDB \\ &=\dfrac12\stackrel{\Large \frown}{AD}+\dfrac12\stackrel{\Large \frown}{BC} \\ & =\dfrac12(\stackrel{\Large \frown}{AD}+\stackrel{\Large \frown}{BC}) \end{array}$
$$圖三$$
觀念影片
|
8
|
(8)圓內角之意義與性質7:04 |
|

