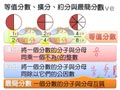
等值分數、擴分、約分與最簡分數

等值分數：設 $a$ 、 $b$ 、 $c$ 、 $d$ 都是整數，若 $\dfrac{a}{b}=\dfrac{c}{d}$ ，則稱 $\dfrac{a}{b}$ 與 $\dfrac{c}{d}$ 為等值分數。

例 $\because \dfrac12=\dfrac24=\dfrac48 \quad$ $\therefore \dfrac12$ 、 $\dfrac24$ 、 $\dfrac48$ 為等值分數

擴分：將一個分數的分子與分母同乘一個不為 $0$ 的整數，此過程稱為擴分。

例 $\dfrac12=\dfrac{1\times 2}{2\times 2}=\dfrac24$

約分：將一個分數的分子與分母同除以它們的公因數，此過程稱為約分。

例 $\dfrac48=\dfrac{4\div 2}{8\div 2}=\dfrac24$

最簡分數：一個分數的分子與分母互質，則此分數為最簡分數。

例 $\dfrac12$ 、 $\dfrac34$ 、 $-\dfrac54$ 、 $\dfrac{-6}{7}$ 為最簡分數