三角形的三邊長不等關係之推導

說明

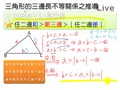
如圖， $\triangle ABC$ 的三邊長分別為 $a$ 、 $b$ 、 $c$ ，則：

$\begin{cases} b+c\gt a \cdots ① \\ c+a\gt b \cdots ② \\ a+b\gt c \cdots ③ \end{cases}$

由 $②$ 式得 $a\gt b-c \cdots ④$

由 $③$ 式得 $a\gt c-b \cdots ⑤$

由 $④$ 、 $⑤$ 式得 $a\gt |b-c| \cdots ⑥$

由 $①$ 、 $⑥$ 式得 $b+c\gt a \gt |b-c|$

同理可得 $c+a\gt b \gt |c-a|$ ， $a+b\gt c \gt |a-b|$ 。