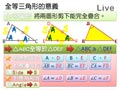
全等三角形的意義
全等圖形:將兩個圖形剪下,能夠完全疊合的幾何圖形稱為全等圖形。
三角形的全等:將兩個三角形剪下疊合,若它們所有的頂點、邊、角都完全重合,就稱這兩個三角形全等。此時重合的頂點稱為對應點,重合的邊稱為對應邊,重合的角稱為對應角。
例 如圖,若 $\triangle ABC$ 與 $\triangle DEF$ 全等,則:
對應點重合: $A$ 與 $D$ 、 $B$ 與 $E$ 、 $C$ 與 $F$ 是三組對應頂點。
對應邊等長: $\overline{AB}=\overline{DE}$ , $\overline{BC}=\overline{EF}$ , $\overline{CA}=\overline{FD}$ 。
對應角相等: $\angle A=\angle D$ , $\angle B=\angle E$ , $\angle C=\angle F$ 。
全等表示法:若 $\triangle ABC$ 全等於 $\triangle DEF$ ,可記為「 $\triangle ABC \cong \triangle DEF$ 」。
符號的記法:我們用英文字母「 $S$ 」表示三角形的邊( Side );用英文字母「 $A$ 」表示三角形的角( Angle )。
觀念影片
|
1
|
(1)全等三角形的意義8:25 |
|

