三角形AAA與SSA不是全等性質之討論
在 $\triangle ABC$ 與 $\triangle DEF$ 中,若 $\angle A=\angle D$ , $\angle B=\angle E$ , $\angle C=\angle F$ ,則 $\triangle ABC$ 與 $\triangle DEF$ 不一定全等,所以三角形 $AAA$ 不是全等性質。
說明
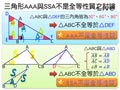
如圖一,在 $\triangle ABC$ 與 $\triangle DEF$ 中,若 $\angle A=\angle D=60^{\circ}$ , $\angle B=\angle E=90^{\circ}$ , $\angle C=\angle F=30^{\circ}$ ,但 $\triangle ABC$ 與 $\triangle DEF$ 並不全等。
$$圖一$$
在 $\triangle ABC$ 與 $\triangle DEF$ 中,若 $\overline{AB}=\overline{DE}$ , $\overline{AC}=\overline{DF}$ , $\angle B=\angle E$ ,則 $\triangle ABC$ 與 $\triangle DEF$ 不一定全等,所以三角形 $SSA$ 不是全等性質。
說明
如圖二,在 $\triangle ABC$ 與 $\triangle ABD$ 中,若 $\overline{AB}=\overline{AB}$ , $\overline{AC}=\overline{AD}$ , $\angle B=\angle B$ ,但 $\triangle ABC$ 與 $\triangle ABD$ 並不全等。
$$圖二$$
觀念影片
|
6
|
(6)三角形AAA與SSA不是全等性質之討論8:10 |
|

