三角形的內角與外角

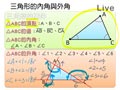
三角形：如圖一，連接不在同一直線上三個點 $A$ 、 $B$ 、 $C$ ，可形成一個三角形，記為「 $\triangle ABC$ 」。

1. $A$ 、 $B$ 、 $C$ 稱為 $\triangle ABC$ 的頂點。
2. $\overline{AB}$ 、 $\overline{BC}$ 、 $\overline{CA}$ 稱為 $\triangle ABC$ 的邊。
3. $\angle A$ 、 $\angle B$ 、 $\angle C$ 稱為 $\triangle ABC$ 的內角。

三角形的外角：

如圖二， $\angle 1$ 是由 $\overline{CA}$ 邊的延長線和 $\overline{AB}$ 邊所形成的角，稱為 $\angle A$ 的一個外角。同理， $\angle 2$ 是 $\angle B$ 的一個外角， $\angle 3$ 是 $\angle C$ 的一個外角。

一個三角形的內角有兩個外角，它們互為對頂角，如圖三， $\angle 4$ 、 $\angle 5$ 、 $\angle 6$ 也分別是 $\angle A$ 、 $\angle B$ 、 $\angle C$ 的另一組外角。

例 如圖四， $\angle 1+\angle A=180^{\circ}$ ， $\angle 2+\angle B=180^{\circ}$ ，$\angle 3+\angle C=180^{\circ}$ 。