多邊形的外角和

說明

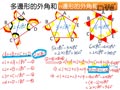
如圖， 五邊形 $ABCDE$ 的內角和 $=\angle 1+\angle 2+\angle 3+\angle 4+\angle 5=180^{\circ}\times 3=540^{\circ}$

$\because (\angle 1+\angle 6)+(\angle 2+\angle 7)+(\angle 3+\angle 8)+(\angle 4+\angle 9)+(\angle 5+\angle 10)=180^{\circ}\times 5=900^{\circ}$

$\Rightarrow 540^{\circ}+(\angle 6+\angle 7+\angle 8+\angle 9+\angle 10=900^{\circ}$

$\Rightarrow \angle 6+\angle 7+\angle 8+\angle 9+\angle 10=900^{\circ}-540^{\circ}=360^{\circ}$