幾何圖形之輔助線

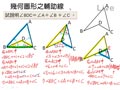
例 如圖，試說明 $\angle BDC=\angle A+\angle B+\angle C$ 。

在原圖上作一條輔助線 $\overline{BC}$ ，

設 $\angle DBC=\angle 1$ ， $\angle DCB=\angle 2$

在 $\triangle BDC$ 中，

$\angle BDC+\angle 1+\angle 2=180^{\circ} \cdots ①$

在 $\triangle ABC$ 中，

$\angle A+\angle B+\angle 1+\angle 2+\angle C=180^{\circ} \cdots ②$

由 $①$ 、 $②$ 得

$\angle BDC+\angle 1+\angle 2=\angle A+\angle B+\angle 1+\angle 2+\angle C$

$\Rightarrow \angle BDC=\angle A+\angle B+\angle C$