三角形外角和定理之推導
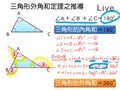
三角形的內角和定理:任意三角形的一組外角和為 $360^{\circ}$ 。
說明
如圖, $\angle 1$ 、 $\angle 2$ 、 $\angle 3$ 分別是 $\angle A$ 、 $\angle B$ 、 $\angle C$ 的一組外角, 因為三角形的一個外角與它的內角互補。
所以
$\begin{array} {l} \angle 1+\angle A=180^{\circ} \; \cdots ① \\ \angle 2+\angle B=180^{\circ} \; \cdots ② \\ \angle 3+\angle C=180^{\circ} \; \cdots ③ \end{array}$
由 $①+②+③$ 得
$\begin{array} {rl} &(\angle 1+\angle A)+(\angle 2+\angle B)+(\angle 3+\angle C)=180^{\circ} \times 3 \\ \Rightarrow & \angle 1+\angle 2+\angle 3+\angle A+\angle B+\angle C=540^{\circ} \\ \Rightarrow & \angle 1+\angle 2+\angle 3+180^{\circ}=540^{\circ} \quad (\because 三角形的內角和=180^{\circ}) \\ \Rightarrow & \angle 1+\angle 2+\angle 3=360^{\circ} \end{array}$
所以 $\triangle ABC$ 的一組外角和為 $360^{\circ}$ 。
觀念影片
|
3
|
(3)三角形外角和定理之推導4:54 |
|

