等差數列第n項公式的推導

設一等差數列的首項為 $a_1$ ，公差為 $d$ ，第 $n$ 項為 $a_n$ ，則 $a_n=a_1+(n-1)d$ 。

說明

$a_2=a_1+d$

$a_3=a_2+d=(a_1+d)+d=a_1+2d$

$a_4=a_3+d=(a_1+2d)+d=a_1+3d$

$\qquad \vdots$

$a_n=a_1+(n-1)d$

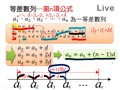
設 $d\gt 0$ ，則等差數列 $a_1$ ， $a_2$ ， $a_3$ ， $\cdots$ ， $a_n$ ，在數線上的圖示如下：

等差數列第n項公式─圖解

觀念影片