相似三角形之判別─SSS相似性質

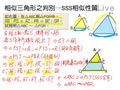
例 如圖， $\triangle ABC$ 與 $\triangle PQR$ 中， $\overline{AB}:\overline{PQ}=\overline{BC}:\overline{QR}=\overline{CA}:\overline{RP}$ ，試說明 $\triangle ABC \sim \triangle PQR$ 。

說明

在 $\overline{PQ}$ 上取一點 $S$，使得 $\overline{PS}=\overline{AB}$ 。

過 $S$ 作平行線交 $\overline{PR}$ 於 $T$ $\Rightarrow \overline{ST}\; /\!/ \;\overline{QR}\;$

$\Rightarrow \; \angle PST=\angle Q$ ， $\angle PTS=\angle R$ （同位角相等）

$\Rightarrow \; \triangle PST \sim \triangle PQR$ （ $AA$ 相似性質）

$\Rightarrow \; \overline{PS}:\overline{PQ}=\overline{ST}:\overline{QR}=\overline{TP}:\overline{RP}\;$ （對應邊成比例）

又 $\because \; \overline{AB}:\overline{PQ}=\overline{BC}:\overline{QR}=\overline{CA}:\overline{RP}\;$

$\Rightarrow \; \overline{AB}=\overline{PS}$ ， $\overline{BC}=\overline{ST}$ ， $\overline{CA}=\overline{TP}$

$\Rightarrow \; \triangle ABC \cong \triangle PST$ （ $SSS$ 全等性質）

又 $\because \; \triangle PST \sim \triangle PQR$

$\therefore \triangle ABC \sim \triangle PQR$ 。