相似三角形的面積比與邊長對應關係比

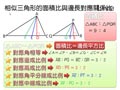
例 如圖，若 $\triangle ABC \sim \triangle PQR$ ，且 $\overline{AB}:\overline{PQ}=3:2$ 。

$\overline{AE}$ 為 $\angle BAC$ 的角平分線， $\overline{AD}$ 與 $\overline{AF}$ 分別為 $\triangle ABC$ 的高與中線。

$\overline{PT}$ 為 $\angle QPR$ 的角平分線， $\overline{PS}$ 與 $\overline{PU}$ 分別為 $\triangle PQR$ 的高與中線，則：

(1) $\overline{AD}:\overline{PS}=\overline{AE}:\overline{PT}=\overline{AF}:\overline{PU}=3:2$

(2) $\triangle ABC 面積：\triangle PQR 面積=3^2:2^2=9:4$