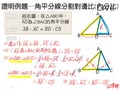
證明例題─角平分線分割對邊比(內分比)

例 如圖一，在 $\triangle ABC$ 中， $\overline{AD}$ 為 $\angle BAC$ 的角平分線，試證： $\overline{AB}:\overline{AC}=\overline{BD}:\overline{CD}$

證明一

過 $C$ 點作一平行 $\overline{AD}$ 的直線交 $\overline{AB}$ 的延長線於 $E$ 點，如圖二所示

$\because \overline{AD}\; /\!/ \;\overline{CE}$

$\therefore \angle 3=\angle 4$（內錯角相等）

$\quad \angle 2=\angle E$（同位角相等）

又 $\because \overline{AD}$ 為 $\angle BAC$ 的角平分線

$\therefore \angle 2=\angle 3 \; \Rightarrow \; \angle 4=\angle E \; \Rightarrow \; \overline{AC}=\overline{AE}$

在 $\triangle BEC$ 中

$\because \overline{AD}\; /\!/ \;\overline{CE}$

$\therefore \overline{BA}:\overline{AE}=\overline{BD}:\overline{DC}$

$\Rightarrow \overline{AB}:\overline{AC}=\overline{BD}:\overline{CD}$

故得證

證明二

過 $D$ 點作 $\overline{DE}\perp \overline{AB}$ ， $\overline{DF}\perp \overline{AC}$ ，如圖三所示

$\because \overline{AD}$ 為 $\angle BAC$ 的角平分線

$\therefore \overline{DE}=\overline{DF}$

$\quad \triangle ABD 面積:\triangle ACD 面積$

$=\dfrac12\times \overline{AB}\times \overline{DE}:\dfrac12\times \overline{AC}\times \overline{DF}$

$=\overline{AB}:\overline{AC}$

過 $A$ 點作 $\overline{AH}\perp \overline{BC}$ ，如圖四所示

$\quad \triangle ABD 面積:\triangle ACD 面積$

$=\dfrac12\times \overline{BD}\times \overline{AH}:\dfrac12\times \overline{CD}\times \overline{AH}$

$=\overline{BD}:\overline{CD}$

$\Rightarrow \overline{AB}:\overline{AC}=\overline{BD}:\overline{CD}$

故得證