一直線截三角形兩邊成比例線段必平行於三角形的第三邊

若一直線截三角形兩邊成比例線段，則此直線必平行於三角形的底邊。

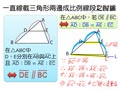
例 如圖一，在 $\triangle ABC$ 中， $D$ 、 $E$ 分別在 $\overline{AB}$ 、 $\overline{AC}$ 上，若 $\overline{AD}:\overline{DB}=\overline{AE}:\overline{EC}$ ，則 $\overline{DE}\; /\!/ \;\overline{BC}$ 。

說明

過 $B$ 點作一直線 $L$ 平行 $\overline{DE}$ 且與直線 $AC$ 相交於 $C'$ 點，如圖二所示，可得 $\overline{AD}:\overline{DB}=\overline{AE}:\overline{EC'}$ ，

$\because \overline{AD}:\overline{DB}=\overline{AE}:\overline{EC}$ (已知)

$\therefore \overline{AE}:\overline{EC}=\overline{AE}:\overline{EC'}$ $\Rightarrow \; \overline{EC}=\overline{EC'}$

$\Rightarrow \; C$ 點與 $C'$ 點重合，故 $\overline{DE}\; /\!/ \;\overline{BC}$ 。