等高三角形的面積比

兩個等高三角形的面積比等於其底邊長度的比。

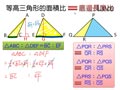
例 如圖一， $\overline{AH}$ 是 $\triangle ABC$ 的高， $\overline{DG}$ 是 $\triangle DEF$ 的高， $\overline{AH}=\overline{DG}$ ，則 $\triangle ABC\,面積:\triangle DEF\,面積=\overline{BC}:\overline{EF}$

說明

$\because \triangle ABC\,面積:\triangle DEF\,面積$

$=\dfrac12\times \overline{BC} \times \overline{AH}:\dfrac12\times \overline{EF} \times \overline{DG}$ ，又 $\overline{AH}=\overline{DG}$

$\therefore \triangle ABC\,面積:\triangle DEF\,面積=\overline{BC}:\overline{EF}$

如圖二，三角形的面積比與其底邊長度比的關係如下：

$\triangle PQR\,面積:\triangle PRS\,面積=\overline{QR}:\overline{RS}$

$\triangle PQR\,面積:\triangle PQS\,面積=\overline{QR}:\overline{QS}$

$\triangle PRS\,面積:\triangle PQS\,面積=\overline{RS}:\overline{QS}$