圓之切線與切線段長性質
切線性質:
- 圓心與切點的連線必和切線垂直。
- 圓心與切點的距離等於圓的半徑。
例 如圖一, $L$ 為圓 $O$ 的切線, $P$ 為切點,圓 $O$ 半徑 $=r$ ,則 $\overline{OP}\perp L$ 且 $\overline{OP}=r$ 。
$$圖一$$
切線段長:如圖二, $P$ 點為圓 $O$ 外一點,由 $P$ 點向圓 $O$ 作一切線,其切點為 $A$ ,則我們稱 $\overline{PA}$ 為 $P$ 點到圓 $O$ 的切線段長。
$$圖二$$
切線段性質:
- 過圓外一點對此圓所作的兩切線段等長。
- 圓外一點與圓心的連線會平分過此點的兩切線夾角。
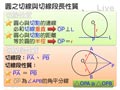
例 如圖三, $P$ 為圓 $O$ 外一點, $\overline{PA}$ 、 $\overline{PB}$ 均為圓 $O$ 的切線, $A$ 、 $B$ 為切點,則 $\overline{PA}=\overline{PB}$ ,且 $\overline{OP}$ 會平分 $\angle APB$ 。
$$圖三$$
觀念影片
|
6
|
(6)圓之切線與切線段長性質10:50 |
|

