畢氏定理(勾股定理)之推導

如$圖一$，直角三角形 $ABC$ 兩股長分別為 $a$ 和 $b$ ，斜邊長為 $c$ 。

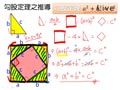
將四個與直角三角形 $ABC$ 相同的直角三角形，和一個邊長為 $c$ 的小正方形，拼成一個邊長為 $a+b$ 的大正方形，如$圖二$。

大正方形面積 $=(a+b)^2=a^2+2ab+b^2$

四個直角三角形的面積和 $=4\times \dfrac12\times a\times b=2ab$

小正方形面積 $=c^2$

由大正方形面積 $-$ 四個直角三角形的面積和 $=$ 小正方形面積

即 $(a^2+2ab+b^2)-2ab=c^2$

$\Rightarrow a^2+b^2=c^2$

$$圖一$$

$$圖二$$