多項式的除法運算_除法關係式

若多項式 $A$ 除以多項式 $B$ ，所得的商式為 $Q$ ，餘式為 $R$ 。

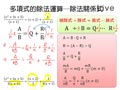
即 $A\div B=Q\cdots R$ ，則有下列關係式：

$A=B\cdot Q+R$

$B=(A-R)\div Q$

$\dfrac{A}{B}=Q+\dfrac{R}{B}$

$\dfrac{mA}{B}=mQ+\dfrac{mR}{B}(m\neq 0)$

$\dfrac{A}{nB}=\dfrac{Q}{n}+\dfrac{R}{nB}(n\neq 0)$

例 $\quad \; (x^2+3x+5)\div (x+1)=(x+2)\cdots 3$

$\Rightarrow (x^2+3x+5)=(x+1)\cdot (x+2)+3$

$\Rightarrow (x+1)=[(x^2+3x+5)-3]\div (x+2)$

$\Rightarrow \dfrac{(x^2+3x+5)}{(x+1)}=(x+2)+\dfrac{3}{(x+1)}$

$\Rightarrow \dfrac{2(x^2+3x+5)}{(x+1)}=2(x+2)+\dfrac{2\cdot 3}{(x+1)}$

$\Rightarrow \dfrac{(x^2+3x+5)}{3(x+1)}=\dfrac{(x+2)}{3}+\dfrac{3}{3(x+1)}$