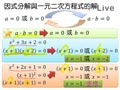
因式分解與一元二次方程式的解

當 $a=0$ 或 $b=0$ 時，$a\cdot b=0$ 。

若 $a\cdot b=0$ ，則 $a=0$ 或 $b=0$ 。利用此法則，將一元二次方程式分解成兩個一次式的乘積等於 $0$ 時，即可求出此方程式的解。

若 $(ax+b)(cx+d)=0$ ，則 $ax+b=0$ 或 $cx+d=0$ ，即 $x=\dfrac{-b}{a}$ 或 $x=\dfrac{-d}{c}$

例 解一元二次方程式 $x^2+3x+2=0$

解 $x^2+3x+2=0$ $\Rightarrow (x+1)(x+2)=0$

$\Rightarrow x+1=0$ 或 $x+2=0$ $\Rightarrow x=-1$ 或 $x=-2$

所以 $x^2+3x+2=0$ 的解為 $x=-1$ 與 $x=-2$

例 解一元二次方程式 $x^2+2x+1=0$

解 $x^2+2x+1=0$ $\Rightarrow (x+1)^2=0$ $\Rightarrow (x+1)(x+1)=0$

$\Rightarrow x+1=0$ 或 $x+1=0$ $\Rightarrow x=-1$ 或 $x=-1$

所以 $x^2+2x+1=0$ 的解為 $x=-1$ （重根）

★ 當一元二次方程式有兩個相同的解，就稱這兩個解為一元二次方程式的重根或等根。